Lecture: Nonconvex Optimization for Deep Learning
University of Tübingen, Wintersemester 2025/2026
Dr. Antonio Orvieto, ELLIS Principal Investigator at MPI.
Time/Date
Tübingen AI center TTR2 lecture hall (Maria-von-Linden-Straße 6) - on Tuesday, 16-18 (lecture) + 18-19 (tutorial)
Exercise Sessions start in the second week.
Coming to the lecture in person is advised, yet I will try to record each session.
Contact
For communication purposes, please use my ELLIS email only.
For feedback or to report errors in slides, please use this form.
TLDR;
Take this module if
- You know what deep learning is, and that deep models are trained with variants of SGD;
- You are curious to understand what influences training speed and generalization in vision and language models.
- Want to know about recent topics such as the NTK, edge of stability, maximum-update parametrization (muP), and Muon.
- You like maths and want to know more about deep learning theory.
Material
All can be found at https://drive.google.com/drive/folders/1ZasVKDEM02UiLAOviv9eZy8wROB9l0ck
Lecture notes from last year (content changed a bit) are also available. Those are curated by Gwendolyn Neitzel, our top student last year.
Basic Information
Note: This lecture does not overlap with "Convex and Nonconvex Optimization." While students are encouraged to take "Convex and Nonconvex Optimization" to solidify their understanding of SGD and basic optimization concepts (duality, interior point methods, constraints), we will only discuss optimization in the context of training deep neural networks and often drift into discussions regarding model design and initialization.
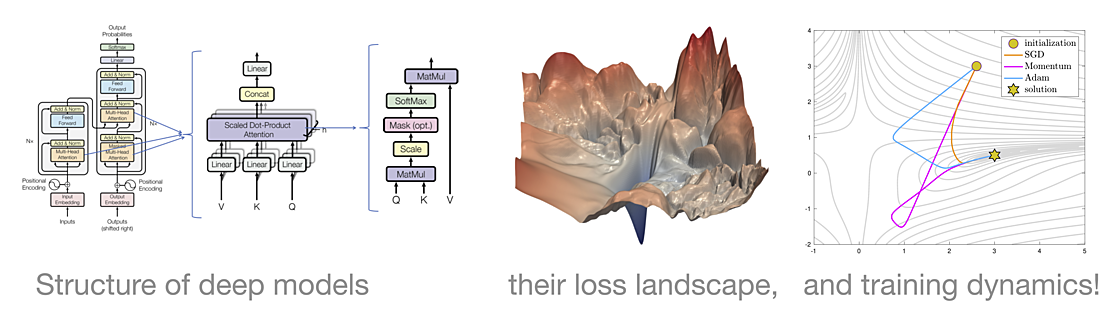
Successful training of deep learning models requires non-trivial optimization techniques. This course gives a formal introduction to the field of nonconvex optimization by discussing training of large deep models. We will start with a recap of essential optimization concepts and then proceed to convergence analysis of SGD in the general nonconvex smooth setting. Here, we will explain why a standard nonconvex optimization analysis cannot fully explain the training of neural networks. After discussing the properties of stationary points (e.g., saddle points and local minima), we will study the geometry of neural network landscapes; in particular, we will discuss the existence of "bad" local minima.
Next, to gain some insight into the training dynamics of SGD in deep networks, we will explore specific and insightful nonconvex toy problems, such as deep chains and matrix factorization/decomposition/sensing. These are to be considered warm-ups (primitives) for deep learning problems. We will then examine training of standard deep neural networks and discuss the impact of initialization and (over)parametrization on optimization speed and generalization. We will also touch on the benefits of normalization and skip connections.
Finally, we will analyze adaptive methods like Adam and discuss their theoretical guarantees and performance on language models. If time permits, we will touch on advanced topics such as label noise, sharpness-aware minimization, neural tangent kernel (NTK), and maximal update parametrization (muP).
Here are a few crucial papers discussed in the lecture (math will be greatly simplified): https://arxiv.org/abs/1605.07110, https://arxiv.org/pdf/1802.06509, https://arxiv.org/abs/1812.0795, https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf,
https://arxiv.org/abs/1502.01852, https://arxiv.org/pdf/2402.16788v1.
Requirements
The course requires some deep learning familiarity and basic knowledge of gradient-based optimization. Students who have already attended "Convex and Nonconvex Optimization" or any machine learning lecture that discusses gradient descent will have no problem following the lecture. In general, the semester requires good mathematical skills, roughly at the level of the lecture "Mathematics for Machine Learning." In particular, multivariate calculus and linear algebra are needed.
Exercises
Exercise sheets will be provided every week and discussed during the next session. Exercises are not graded, and no project has been planned.
Exam
Written exam, 2h, closed book. This is 100% of your grade.
Schedule (Tentative)
-
October 14 — Lecture 0 - Intro + Linear Regression
-
October 21 — Lecture 1 - SGD on Convex Quadratics
-
October 28 — Lecture 2 - Neural Nets Universality + Signal Propagation
-
November 4 — Lecture 3 - Initialization and Saddle Points
-
November 11 — Lecture 4 - Nonconvex SGD Analysis
-
November 18 — Lecture 5 - Sharpness, Flat Minima and Generalization
- November 25 — Canceled
-
December 2 — Lecture 6 - Feature learning, NTK, and muP
- December 9 — Canceled
-
December 16 — Lecture 7 - Overparametrization
- December 23 — Break
- December 30 — Break
- January 6 — Break
-
January 13 — Lecture 8 - Skip Connections and Layer Norm
-
January 20 — Lecture 9 - Adaptive Stepsizes (Adagrad, Polyak)
-
January 27 — Lecture 10 - Adaptive Stepsizes (Adam, Muon)
-
February 3 — Lecture 11 - Scaling Laws